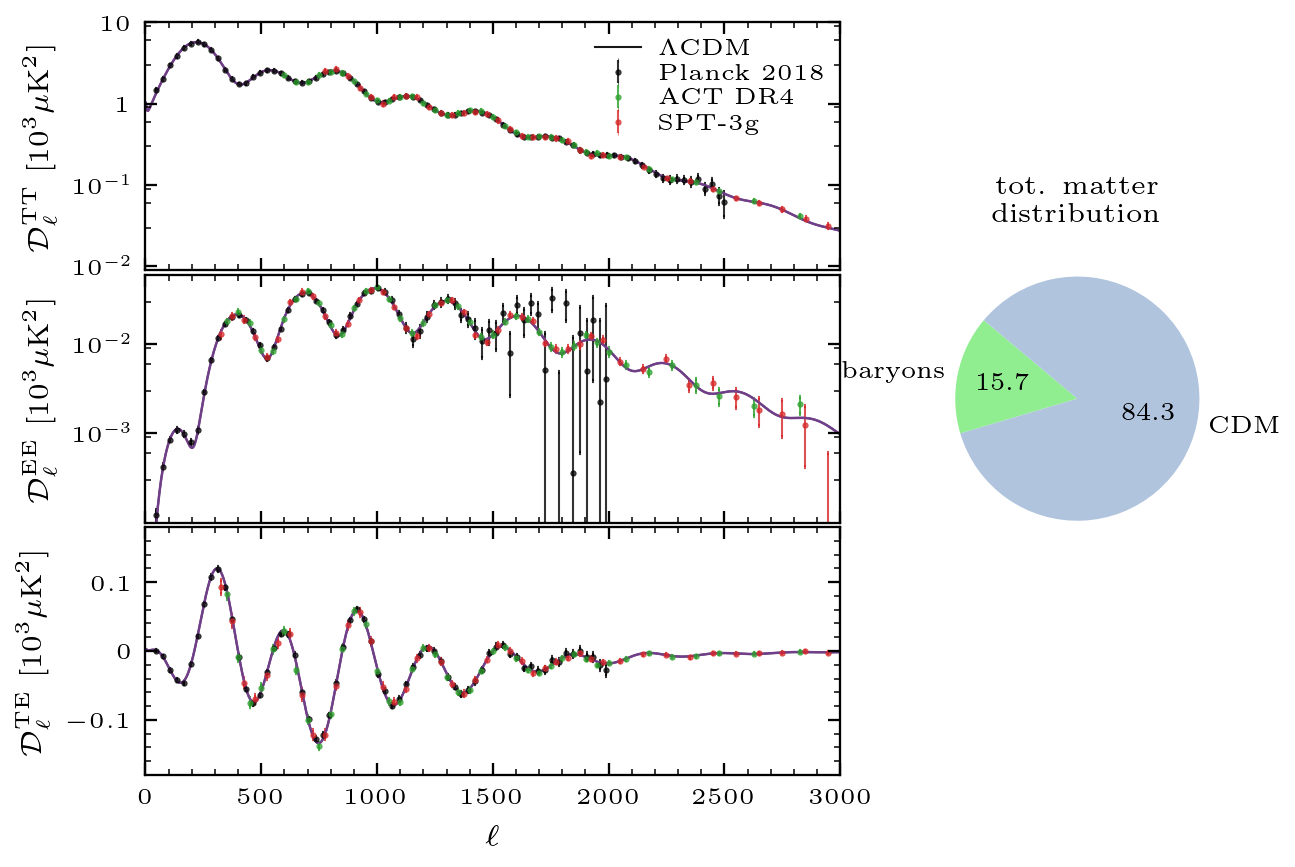
Baryons and Dark Matter
The total matter density in the universe is a crucial parameter in the evolution of the primordial plasma, primarily through its influence on the expansion rate and its role in sourcing the gravitational potential wells that seed structure in the universe. Specifically, the patterns of fluctuations in the CMB require both a pressure-supported and a pressureless form of matter. The former, known as baryons, consists primarily of electrons and protons, which are strongly coupled to photons in the early universe. The inertia of these particles consequently slows down the sound waves in the fluid, while photon pressure counteracts their gravitational collapse. This is why an additional, pressureless form of matter—dark matter—is essential, as it clusters freely under gravity without resistance from photon pressure, enhancing the initial fluctuations and seeding the growth of cosmic structure.
By holding the density of baryonic matter \(\omega_{b}\) constant while allowing for the density of dark matter \(\omega_{CDM}\) to vary, we can isolate the effects of a collisionless matter component, dark matter, while also highlighting the sensitivity of the CMB to changes in the total matter density. With less dark matter, the gravitational potential wells in which the photon-baryon fluid propagates become shallower. Thus the outward photon pressure is less effectively counteracted by gravity, a mechanism known as radiation driving. This drives acoustic oscillations to oscillate with greater amplitudes, resulting in increased oscillation amplitudes at lower angular scales. Additionally, a decreased matter density also moves the moment of matter-radiation equality in the universe to a later time; during this time, the gravitational potential wells decay. This results in a boost in the amplitude of perturbations in the photon-baryon fluid traveling through these wells, an effect called the early Integrated Sachs-Wolfe (ISW) effect. This time dependence deviates from zero only at large scales, thus the effect further contributes to an increase in amplitude for the first few peaks.
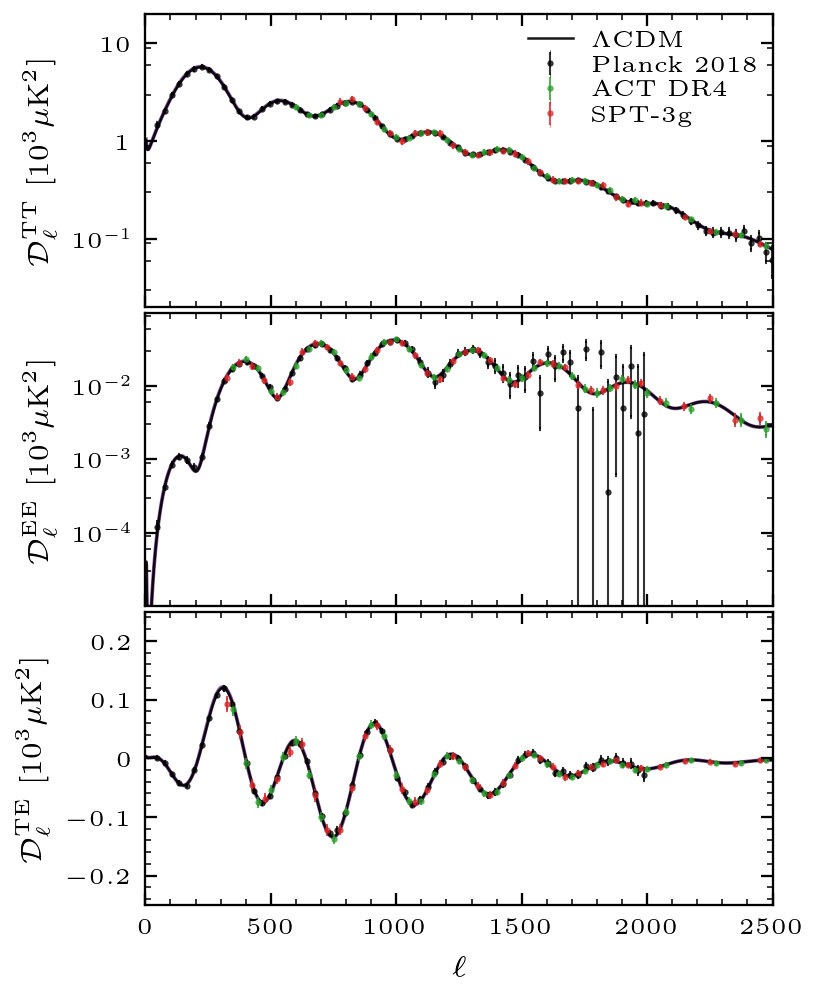
Next, we examine the effects of varying the relative proportions of pressure-supported and pressureless forms of matter while maintaining the same moment of radiation and matter equality. This approach removes the effects of a varying total matter energy density and isolates the influence of the baryonic-dark matter balance on acoustic oscillations in the CMB. We vary the amount of baryonic matter in the universe while inversely adjusting the dark matter concentration so that the total matter concentration maintains its fiducial value. Firstly, whereas dark matter effectively only increases the depth of potential wells as a whole, the coupled baryonic matter also drags down the oscillations. This baryon loading results in an influence on the equilibrium position of acoustic waves in the photon-baryon plasma. Thus, a greater baryonic matter density would enhance the amplitude of odd peaks (representing contraction) relative to even peaks (representing rarefaction). Additionally, there is an observed damping effect with more baryonic matter. This stems from a choice to fix the position of the first peak to reflect its well-measured angular scale, which is our best indication of the flatness of the universe. The total dark energy must then increase with the baryonic matter energy density to maintain this flatness, which results in an increase in cosmic expansion (measured by Hubble's constant,\(H\)). If we fix the sound horizon at the surface of last scattering \(\theta_s\), then the angular scale at which diffusion damping occurs should increase by the proportionality:
\( \theta_d \propto H^{1/2} \theta_s \)
Thus, an increase in baryonic matter density results in damping at larger angular scales, corresponding to smaller multipoles.