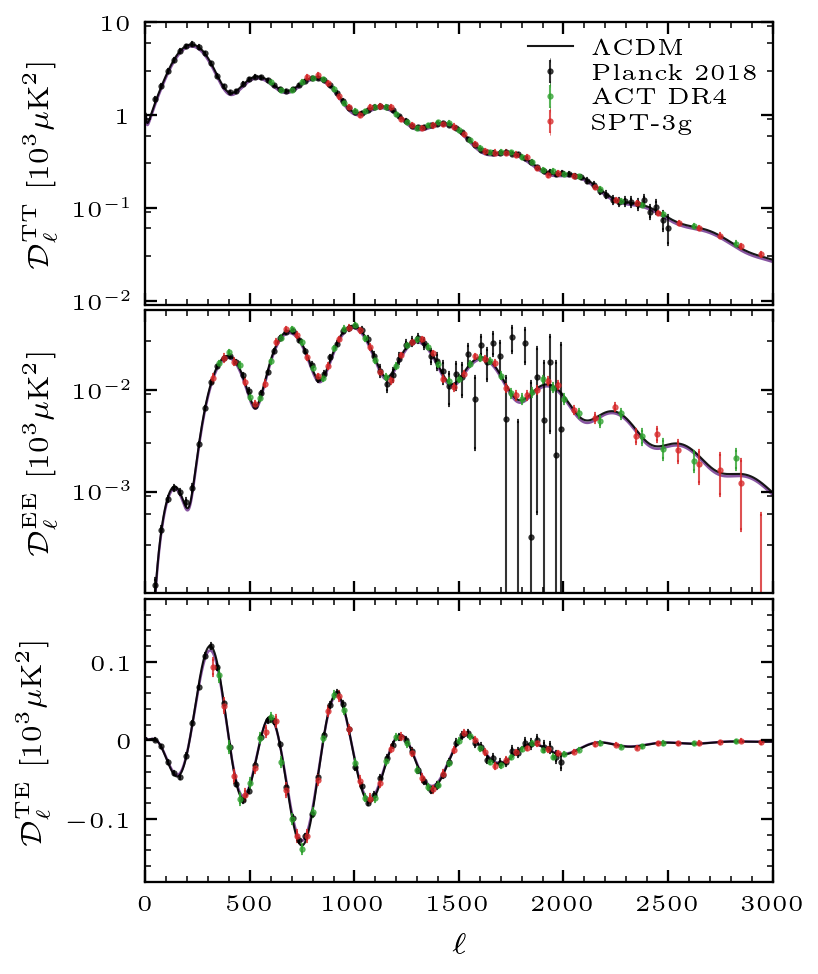
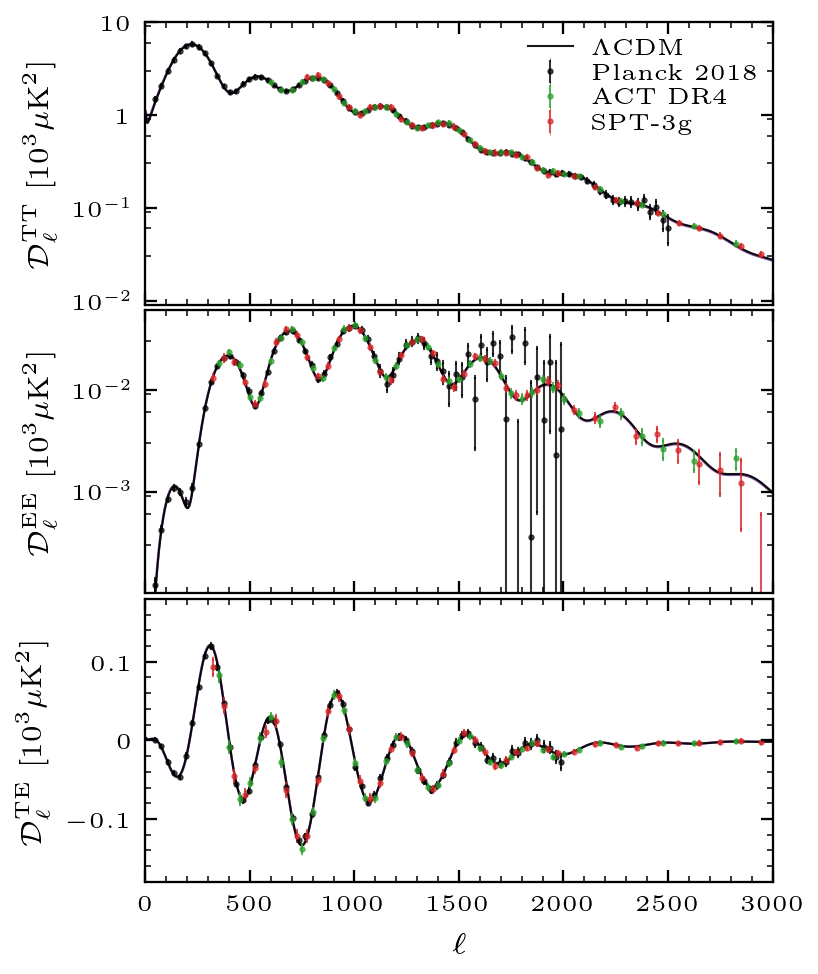
Primordial Power Spectrum

In the context of the \( \Lambda\rm{CDM} \) model, we introduce the spectrum of primordial curvature perturbations to describe the initial density fluctuations that excited sound waves in the primordial plasma, which we ultimately observe today as temperature and polarization fluctuations in the CMB.

The primordial curvature power spectrum is generically expressed as a power law in k, according to:

\( \Delta^2_{\mathcal{R}} (k) = A_s \left( \frac{k}{k_\star}\right )^{n_s-1} \)

where \(A_s\) and \(n_s\) represent respectively the amplitude and spectral index of the spectrum, while \(k _\star \) is an arbitrarly chosen pivot scale, tipically set to 0.05 Mpc\(^{-1}\) in the context of CMB experiments.

The amplitude, \(A_s\), sets the overall scale of the initial fluctuations, which in turn determines the amplitude of the observed CMB anisotropies. A higher \(A_s\) results in larger temperature and polarization fluctuations, and viceversa. On the other hand, \(n_s\) controls how the amplitude of these fluctuations changes with scale. If \(n_s = 1\), the fluctuations are "scale-invariant," meaning they have the same power across all scales. Values of \(n_s\) slightly less than 1, as observed, indicate more power on larger scales (smaller multipoles), whereas for \(n_s>1\), the tilt of the CMB power spectra moves upward as more power goes to smaller scales (larger multipoles).