Neutrinos

In the standard model of particle physics, neutrinos constitute a significant fraction of the radiation density in the early universe. As the weakest coupled particles in the Standard Model, they decoupled from the primordial plasma roughly one second after the Big Bang and have been free-streaming ever since. The Cosmic Microwave Background (CMB) is gravitationally sensitive to this background of cosmic neutrinos, responding to both their total energy density and their free-streaming nature. Their contribution is typically parameterized by the effective number of relativistic species, \(N_{\rm eff}\). This parameter relates the neutrino energy density to that of photons. In the Standard Model, assuming instantaneous decoupling, \(N_{\rm eff}\) would be 3. However, after accounting for the slightly delayed decoupling process and small quantum corrections, the precise Standard Model prediction becomes \(N_{\rm eff}=3.044\).

Effective Number of Neutrino Species (\(N_{\rm eff}\))

The most significant effect of cosmic neutrinos arises from their contribution to the background energy density, which influences the Hubble expansion rate. If we fix the sound horizon at the surface of last scattering \(\theta_s\), then the angular scale at which diffusion damping occurs increases according to:

\( \theta_d \propto H^{1/2} \theta_s \)

Thus, a larger value of (\(N_{\rm eff}\)) corresponds to a larger Hubble expansion rate and thus more damping at larger angular scales, corresponding to smaller multipoles. We show this effect explictly in the plot below, where we hold fixed both \(\theta_s\), \(a_{eq}\) and \(\omega_b\).

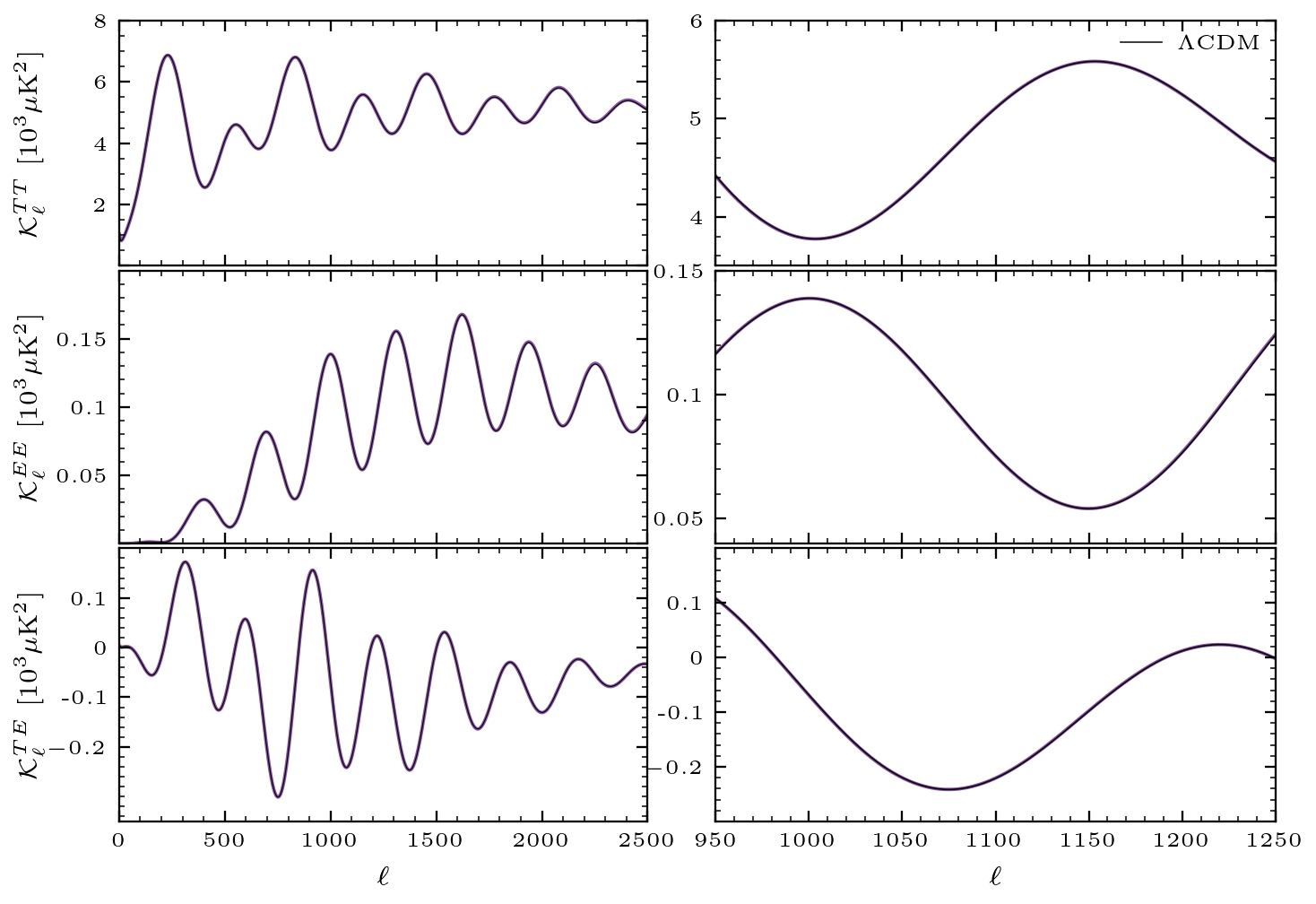
Beyond their energy density, a critical feature of the neutrinos is that they are free-streaming, and by doing so, they induce metric perturbations ahead of the sound horizon. This manifests as a small phase shift in the CMB power spectra, whose magnitude is proportional to the fraction of radiation energy contained in neutrinos. Schematically, we can understand this as follows: neutrinos are free-streaming essentially at the speed of light and thus overtake the photons (which instead move much slower as they are tightly coupled to the baryons prior to recombination) and then gravitationally pull them slightly ahead of the sound horizon to larger radii. As illustrated below, we in fact see that increasing \\(N_{\\rm{eff}}\\) shifts the peaks of the CMB power spectra toward lower multipoles (i.e., larger angular scales).

Note, in order to isolate this small effect, in addition to fixing the values of \(\theta_s\), \(a_{\rm eq}\) and \(\omega_b\), we also fixed the damping scale \(\theta_d\) by appropriately rescaling the primordial Helium fraction \(Y_{p}\), as well as undamp the spectra and normalize them to the correspondig amplitude at the fourth peak. Specifically we display:

\[ \mathcal{K}^{XY}_\ell = \frac{\ell (\ell+1)}{2\pi} C^{XY}_\ell \exp\{a\,(\theta_d \ell)^\kappa\} \]

where \(\theta_d\approx 1.3\times 10^{-3}\) is the fiducial damping scale and \(a\approx 0.68\) and \(\kappa\approx 1.3\) are the fitting parameters to effectively remove the exponential diffusion damping.

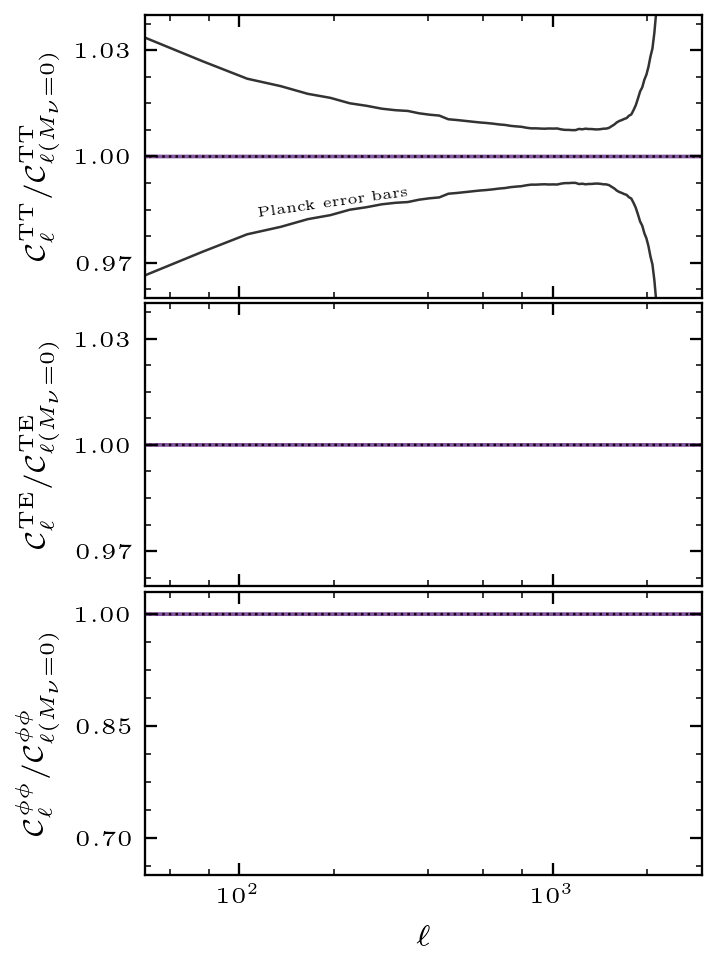
Neutrino Masses (\(M_{\nu}\))

Another gravitationally relevant property of neutrinos is that they are massive, which means that at late times they contribute to the total matter density of the universe. For light neutrino masses below 1 eV — those allowed by current CMB observations — their relativistic speeds suppress the matter power spectrum. This suppression reduces the gravitational lensing experienced by CMB photons as they travel from the last scattering surface to the present day. As a result, we observe sharper peaks in the CMB power spectra and a reduced amplitude in the lensing potential at small scales.

The panels below illustrate these effects by showing the residuals between the predictions of the standard \(\Lambda\)CDM model with massless and massive neutrinos. Notice the oscillatory features in the temperature spectra residuals at small scales and the overall suppression of the lensing spectrum. These signatures provide crucial information about neutrino masses and their cosmological effects. While this discussion focuses on these primary effects, it is worth noting that many details - such as the exact mass hierarchy - remain subjects of ongoing research.